11. Sınıf Matematik 1.Dönem 1. Yazılı Soruları Örneği
Soru 1:
Aşağıda derece türünden açı değerleri verilen bazı açıların karşılarına radyan türünden değerleri yazılmıştır.
Buna göre, bu eşleştirmelerden hangileri doğrudur?
| Derece | Radyan |
|---|---|
| I. 135° | \( \frac{3\pi}{4} \) |
| II. 330° | \( \frac{11\pi}{12} \) |
| III. 150° | \( \frac{3\pi}{5} \) |
Çözüm: Not: \( Radyan = \frac{\pi.Derece}{180} \)
I. \( R = \frac{\pi.135}{180} = \frac{3\pi}{4} \)
II. \( R = \frac{\pi.330}{180} = \frac{11\pi}{6} \)
III. \( R = \frac{\pi.150}{180} = \frac{5\pi}{6} \)
I doğru, II ve III yanlış
I. \( R = \frac{\pi.135}{180} = \frac{3\pi}{4} \)
II. \( R = \frac{\pi.330}{180} = \frac{11\pi}{6} \)
III. \( R = \frac{\pi.150}{180} = \frac{5\pi}{6} \)
I doğru, II ve III yanlış
Soru 2:
α = 21° 33′ 21″
β = 5° 11′ 53″
olduğuna göre; α – 2β işleminin sonucu kaçtır?
Çözüm:
β = 5° 11′ 53″
2β = 10° 22′ 106″
α – 2β = 21° 33′ 21″ – (10° 22′ 106″)
α – 2β = 21° 31′ 141″ – (10° 22′ 106″)
α – 2β = 11° 9′ 35″
α = 21° 33′ 21″
β = 5° 11′ 53″
2β = 10° 22′ 106″
α – 2β = 21° 33′ 21″ – (10° 22′ 106″)
α – 2β = 21° 31′ 141″ – (10° 22′ 106″)
α – 2β = 11° 9′ 35″
Soru 3:
\(A = \frac{24π}{5}\) ve \(B = 2250°\)
olduğuna göre, A + B toplamının esas ölçüsü kaç derecedir?
Çözüm: Önce A açısının esas ölçüsünü bulalım.
\(A = \frac{24π}{5} = 4\pi + \frac{4\pi}{5} \)
A açısının esas ölçüsü: \( \frac{4\pi}{5} = 144° \)
Şimdi B açısının esas ölçüsünü bulalım:
\(B = 2250° = 6.360° + 90°\)
B açısının esas ölçüsü: \( 90° \)
\(A+B = 144 +90 = 234° \)
\(A+B\) nin esas ölçüsü: \(234°\)
\(A = \frac{24π}{5} = 4\pi + \frac{4\pi}{5} \)
A açısının esas ölçüsü: \( \frac{4\pi}{5} = 144° \)
Şimdi B açısının esas ölçüsünü bulalım:
\(B = 2250° = 6.360° + 90°\)
B açısının esas ölçüsü: \( 90° \)
\(A+B = 144 +90 = 234° \)
\(A+B\) nin esas ölçüsü: \(234°\)
Soru 4:
\( P(a , \frac{1}{2}) \) noktası birim çember üzerinde olduğuna göre, \(a\)’nın alabileceği değerler çarpımı kaçtır?
\( P(a , \frac{1}{2}) \) noktası birim çember üzerinde olduğuna göre, \(a\)’nın alabileceği değerler çarpımı kaçtır?
Çözüm:
P noktası birim çember üzerinde olduğuna göre, çember denklemini sağlar.
\( P(a , \frac{1}{2}) \) birim çember üzerinde olduğuna göre,
\( a^2 + (\frac{1}{2})^2 = 1 \)
\( a^2 + \frac{1}{4} = 1 \)
\( a^2 = 1 – \frac{1}{4} \)
\( a^2 =\frac{3}{4} \)
\( a =\frac{\sqrt{3}}{2} \) veya \( a =-\frac{\sqrt{3}}{2} \) değerlerini alabilir. \( \frac{\sqrt{3}}{2}.(-\frac{\sqrt{3}}{2})\) = \(-\frac{3}{4} \)
P noktası birim çember üzerinde olduğuna göre, çember denklemini sağlar.
\( P(a , \frac{1}{2}) \) birim çember üzerinde olduğuna göre,
\( a^2 + (\frac{1}{2})^2 = 1 \)
\( a^2 + \frac{1}{4} = 1 \)
\( a^2 = 1 – \frac{1}{4} \)
\( a^2 =\frac{3}{4} \)
\( a =\frac{\sqrt{3}}{2} \) veya \( a =-\frac{\sqrt{3}}{2} \) değerlerini alabilir. \( \frac{\sqrt{3}}{2}.(-\frac{\sqrt{3}}{2})\) = \(-\frac{3}{4} \)
Soru 5:
\( \frac{sinx}{cotx + cosecx } – \frac{sinx}{cotx – cosecx} \)
ifadesinin en sade halini bulunuz.
\( \frac{sinx}{cotx + cosecx } – \frac{sinx}{cotx – cosecx} \)
ifadesinin en sade halini bulunuz.
Çözüm:
\( \frac{sinx}{cotx + cosecx } – \frac{sinx}{cotx – cosecx} = \frac{sinx}{\frac{cosx}{sinx} + \frac{1}{sinx} } – \frac{sinx}{\frac{cosx}{sinx} – \frac{1}{sinx}} \)
\( \frac{sinx}{\frac{cosx + 1}{sinx} } – \frac{sinx}{\frac{cos-1}{sinx}} = \frac{sinx.sinx}{cosx + 1} – \frac{sinx.sinx}{cosx-1} \)
paydaları eşitleyelim:
\( \frac{sin^2x(cosx-1)}{(cosx + 1)(cosx-1)} – \frac{sin^2x(cosx+1)}{(cosx + 1)(cosx-1)} \)
\( =\frac{sin^2x(cosx-1)}{(cos^2x – 1)} – \frac{sin^2x(cosx+1)}{(cos^2x – 1)} \)
\( =\frac{sin^2x(cosx-1)}{-sin^2x} – \frac{sin^2x(cosx+1)}{-sin^2x} \)
\( =\frac{(cosx-1)}{-1} – \frac{(cosx+1)}{-1} \)
\( =-cosx+1 + cosx+1 = 2 \)
\( \frac{sinx}{cotx + cosecx } – \frac{sinx}{cotx – cosecx} = \frac{sinx}{\frac{cosx}{sinx} + \frac{1}{sinx} } – \frac{sinx}{\frac{cosx}{sinx} – \frac{1}{sinx}} \)
\( \frac{sinx}{\frac{cosx + 1}{sinx} } – \frac{sinx}{\frac{cos-1}{sinx}} = \frac{sinx.sinx}{cosx + 1} – \frac{sinx.sinx}{cosx-1} \)
paydaları eşitleyelim:
\( \frac{sin^2x(cosx-1)}{(cosx + 1)(cosx-1)} – \frac{sin^2x(cosx+1)}{(cosx + 1)(cosx-1)} \)
\( =\frac{sin^2x(cosx-1)}{(cos^2x – 1)} – \frac{sin^2x(cosx+1)}{(cos^2x – 1)} \)
\( =\frac{sin^2x(cosx-1)}{-sin^2x} – \frac{sin^2x(cosx+1)}{-sin^2x} \)
\( =\frac{(cosx-1)}{-1} – \frac{(cosx+1)}{-1} \)
\( =-cosx+1 + cosx+1 = 2 \)
Soru 6:
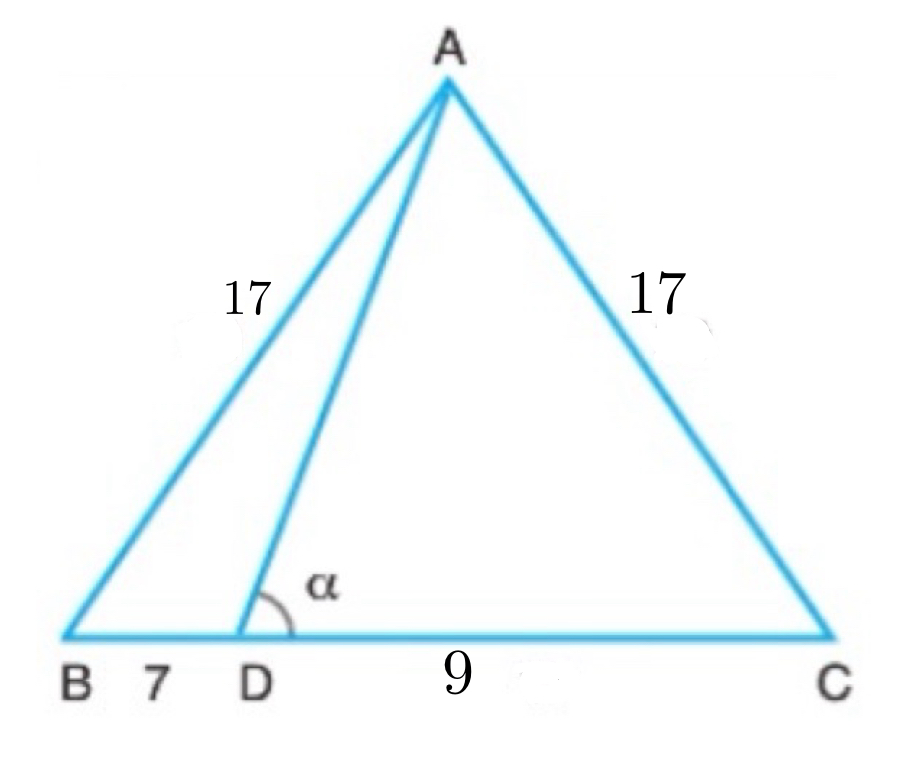
ABC ikizkenar üçgen
|AB| = |AC| = 17 br
|BE| = 7 br
|BC| = 16 br
m(ADC) = α
Yukarıda verilenlere göre, tanα değeri kaçtır?

ABC ikizkenar üçgen
|AB| = |AC| = 17 br
|BE| = 7 br
|BC| = 16 br
m(ADC) = α
Yukarıda verilenlere göre, tanα değeri kaçtır?
Çözüm:
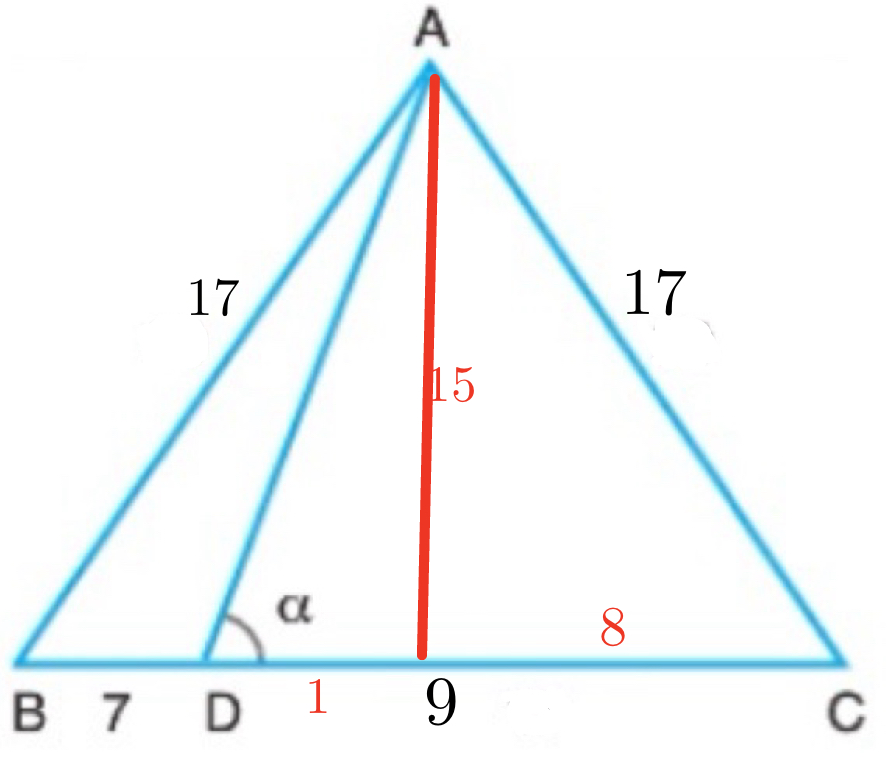
ABC ikizkenar üçgen olduğundan; A noktasından |BC| kenarına dik çizersek bu dik kenarı 2 eşit parçaya böler. Bu diklik noktasına F dersek |BF| = |CF| = 8 br olur. |FD| uzunluğu ise 1 birim olur. |AF| uzunluğu ise 8-15-17 özel üçgeninden 15 br olur. Son olarak Tanα değerini bulalım.
\( tanα = \frac{15}{1} = 15 \)

ABC ikizkenar üçgen olduğundan; A noktasından |BC| kenarına dik çizersek bu dik kenarı 2 eşit parçaya böler. Bu diklik noktasına F dersek |BF| = |CF| = 8 br olur. |FD| uzunluğu ise 1 birim olur. |AF| uzunluğu ise 8-15-17 özel üçgeninden 15 br olur. Son olarak Tanα değerini bulalım.
\( tanα = \frac{15}{1} = 15 \)
Soru 7:
\( \frac{sin(63\pi + x) + cos(70\pi – x)}{cos(\frac{47\pi}{2}-x)+sin(\frac{57\pi}{2}+x)} \)
ifadesinin en sade halini bulunuz.
\( \frac{sin(63\pi + x) + cos(70\pi – x)}{cos(\frac{47\pi}{2}-x)+sin(\frac{57\pi}{2}+x)} \)
ifadesinin en sade halini bulunuz.
Çözüm: Önce radyan türünden verilen açıların esas ölçülerini bulalım.
\( 63\pi = 31.2\pi + \pi\) esas ölçüsü:\(\pi\)
\(70\pi = 35.2\pi\) esas ölçücü: \( 0 \)
\( \frac{47\pi}{2} = 11.2\pi + \frac{3\pi}{2} \) esas ölçüsü: \( \frac{3\pi}{2} \)
\( \frac{57\pi}{2} = 14.2\pi + \frac{\pi}{2} \) esas ölçüsü: \( \frac{\pi}{2} \)
\( \frac{sin(\pi + x) + cos(-x)}{cos(\frac{3\pi}{2}-x)+sin(\frac{\pi}{2}+x)} \)
\( \frac{-sin(x) + cos(x)}{-sin(x)+cos(x)} = 1 \)
\( 63\pi = 31.2\pi + \pi\) esas ölçüsü:\(\pi\)
\(70\pi = 35.2\pi\) esas ölçücü: \( 0 \)
\( \frac{47\pi}{2} = 11.2\pi + \frac{3\pi}{2} \) esas ölçüsü: \( \frac{3\pi}{2} \)
\( \frac{57\pi}{2} = 14.2\pi + \frac{\pi}{2} \) esas ölçüsü: \( \frac{\pi}{2} \)
\( \frac{sin(\pi + x) + cos(-x)}{cos(\frac{3\pi}{2}-x)+sin(\frac{\pi}{2}+x)} \)
\( \frac{-sin(x) + cos(x)}{-sin(x)+cos(x)} = 1 \)
Soru 8:
\(\frac{3\pi}{2} < x < 2\pi \) olmak üzere,
\( cotx – \frac{3 + cosx}{sinx} = 5 \)
olduğuna göre, \(cotx\) değeri kaçtır?
\(\frac{3\pi}{2} < x < 2\pi \) olmak üzere,
\( cotx – \frac{3 + cosx}{sinx} = 5 \)
olduğuna göre, \(cotx\) değeri kaçtır?
Çözüm:
\( \frac{cosx}{sinx} – \frac{3 + cosx}{sinx} = 5 \)
\( \frac{cosx-3-cosx}{sinx} = 5 \)
\( \frac{-3}{sinx} = 5 \)
\( -3 = 5.sinx \)
\( sinx = \frac{-3}{5} \)
dar açılarından biri \(x\) olan dik üçgen çizersek 3-4-5 üçgeni olduğunu göreceğiz.
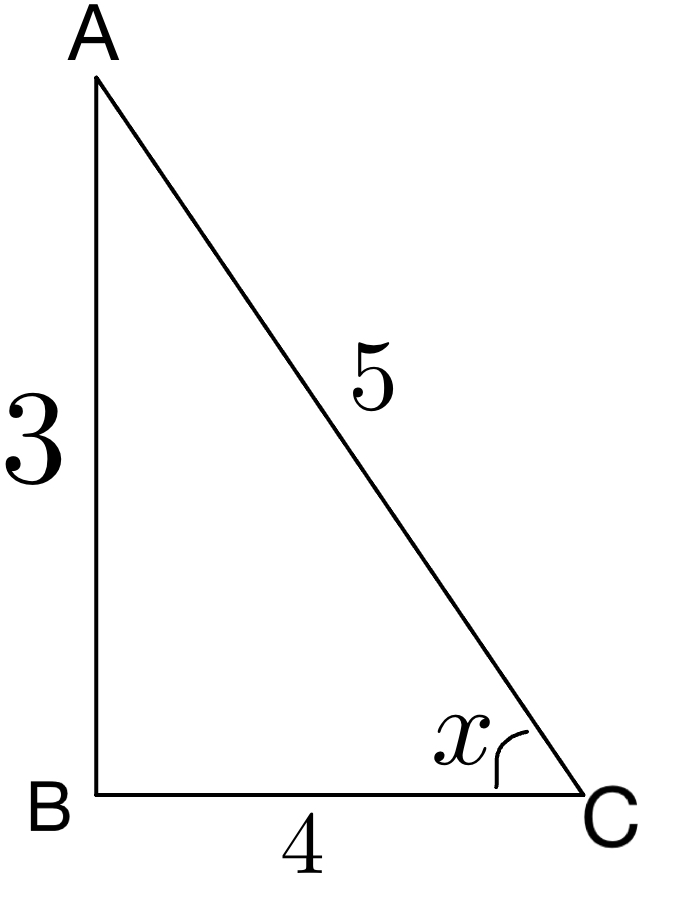
\(x\) açısı 4. bölgede olduğundan \(cotx\) değeri negatif olur.
\( cotx = -\frac{4}{3} \)
\( \frac{cosx}{sinx} – \frac{3 + cosx}{sinx} = 5 \)
\( \frac{cosx-3-cosx}{sinx} = 5 \)
\( \frac{-3}{sinx} = 5 \)
\( -3 = 5.sinx \)
\( sinx = \frac{-3}{5} \)
dar açılarından biri \(x\) olan dik üçgen çizersek 3-4-5 üçgeni olduğunu göreceğiz.

\(x\) açısı 4. bölgede olduğundan \(cotx\) değeri negatif olur.
\( cotx = -\frac{4}{3} \)
Soru 9:
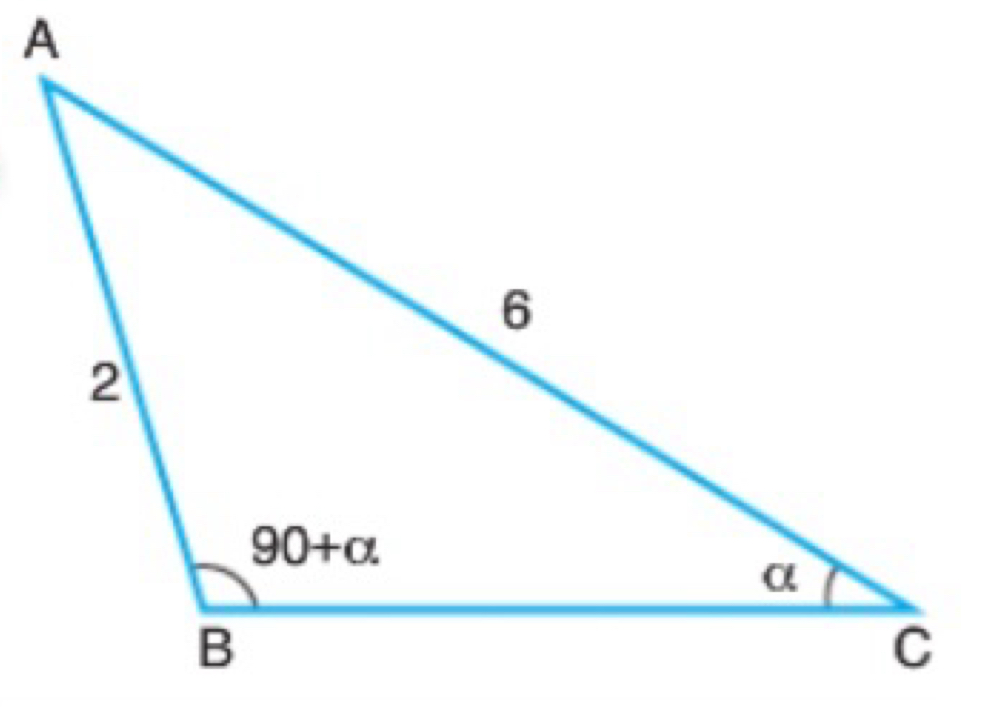
ABC üçgeninde
|AC| = 3|AB| = 6 br
m(ACB) = α
m(ABC) = 90° + α
Yukarıda verilenlere göre, cot(α) değeri kaçtır?

ABC üçgeninde
|AC| = 3|AB| = 6 br
m(ACB) = α
m(ABC) = 90° + α
Yukarıda verilenlere göre, cot(α) değeri kaçtır?
Çözüm:
\( \frac{sinα}{2} = \frac{sin(90+α)}{6} \)
\( \frac{sinα}{2} = \frac{cosα}{6} \)
\( 6.sinα = 2.cosα \)
\( \frac{6}{2} = \frac{cosα}{sinα} \)
\( cotα = 3 \)
\( \frac{sinα}{2} = \frac{sin(90+α)}{6} \)
\( \frac{sinα}{2} = \frac{cosα}{6} \)
\( 6.sinα = 2.cosα \)
\( \frac{6}{2} = \frac{cosα}{sinα} \)
\( cotα = 3 \)
Soru 10:
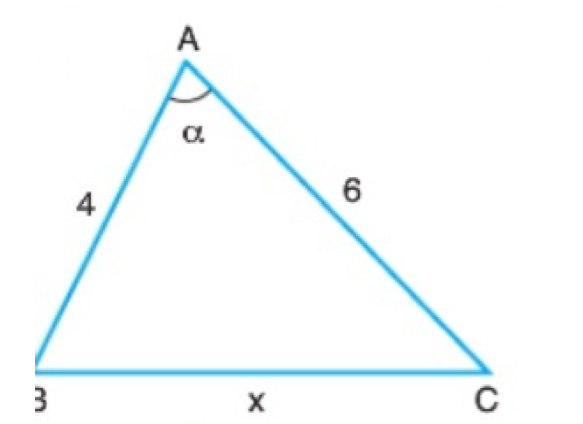
ABC üçgeninde
|AB| = 4 br
|AC| = 6 br
m(BAC) = α
\(cos(α) = \frac{1}{12}\)
olduğuna göre, |BC| = x kaç birimdir?

ABC üçgeninde
|AB| = 4 br
|AC| = 6 br
m(BAC) = α
\(cos(α) = \frac{1}{12}\)
olduğuna göre, |BC| = x kaç birimdir?
Çözüm:
\(x^2 = 4^2 + 6^2 – 2.4.6.cosα \)
\(x^2 = 16 + 36 – 48.\frac{1}{12} \)
\(x^2 = 52 – 4 \)
\(x^2 = 48 \)
\(x = \sqrt{48} \)
\(x = 4\sqrt{3} br\)
\(x^2 = 4^2 + 6^2 – 2.4.6.cosα \)
\(x^2 = 16 + 36 – 48.\frac{1}{12} \)
\(x^2 = 52 – 4 \)
\(x^2 = 48 \)
\(x = \sqrt{48} \)
\(x = 4\sqrt{3} br\)