11. Sınıf Matematik 1.Dönem 1. Yazılı Soruları Örneği
Soru 1:
Aşağıda derece türünden açı değerleri verilen bazı açıların karşılarına radyan türünden değerleri yazılmıştır.
Buna göre, bu eşleştirmelerden hangileri doğrudur?
| Derece | Radyan |
|---|---|
| I. 225° | \( \frac{5\pi}{4} \) |
| II. 240° | \( \frac{4\pi}{3} \) |
| III. 300° | \( \frac{5\pi}{2} \) |
Çözüm: Not: \( Radyan = \frac{\pi.Derece}{180} \)
I. \( R = \frac{\pi.225}{180} = \frac{5\pi}{4} \)
II. \( R = \frac{\pi.240}{180} = \frac{4\pi}{3} \)
III. \( R = \frac{\pi.300}{180} = \frac{5\pi}{3} \)
I ve II doğru III yanlış
I. \( R = \frac{\pi.225}{180} = \frac{5\pi}{4} \)
II. \( R = \frac{\pi.240}{180} = \frac{4\pi}{3} \)
III. \( R = \frac{\pi.300}{180} = \frac{5\pi}{3} \)
I ve II doğru III yanlış
Soru 2:
α = 23° 34′ 17″
β = 4° 12′ 46″
olduğuna göre; 2α – β işleminin sonucu kaçtır?
Çözüm:
\(2α – β = 47° 08^{‘} 34^{“} – 4° 12^{‘} 46^{“} \)
\(2α – β = 46° 67^{‘} 94^{“} – 4° 12^{‘} 46^{“} \)
\(2α – β = 42° 55^{‘} 48^{“} \)
α = 23° 34′ 17″
2.α = 46° 68′ 34″
2.α = 47° 08′ 34″
\(2α – β = 47° 08^{‘} 34^{“} – 4° 12^{‘} 46^{“} \)
\(2α – β = 46° 67^{‘} 94^{“} – 4° 12^{‘} 46^{“} \)
\(2α – β = 42° 55^{‘} 48^{“} \)
Soru 3:
\(A = \frac{19π}{4}\) ve \(B = 1750°\)
olduğuna göre, A + B toplamının esas ölçüsü kaç derecedir?
Çözüm: Önce A açısının esas ölçüsünü bulalım.
\(A = \frac{19π}{4} = 4\pi + \frac{3\pi}{4} \)
A açısının esas ölçüsü: \( \frac{3\pi}{4} = 135° \)
Şimdi B açısının esas ölçüsünü bulalım:
\(B = 1750° = 4.360° + 310°\)
B açısının esas ölçüsü: \( 310° \)
\(A+B = 135 +310 = 445° = 360° + 85°\)
\(A+B\) nin esas ölçüsü: \(85°\)
\(A = \frac{19π}{4} = 4\pi + \frac{3\pi}{4} \)
A açısının esas ölçüsü: \( \frac{3\pi}{4} = 135° \)
Şimdi B açısının esas ölçüsünü bulalım:
\(B = 1750° = 4.360° + 310°\)
B açısının esas ölçüsü: \( 310° \)
\(A+B = 135 +310 = 445° = 360° + 85°\)
\(A+B\) nin esas ölçüsü: \(85°\)
Soru 4:
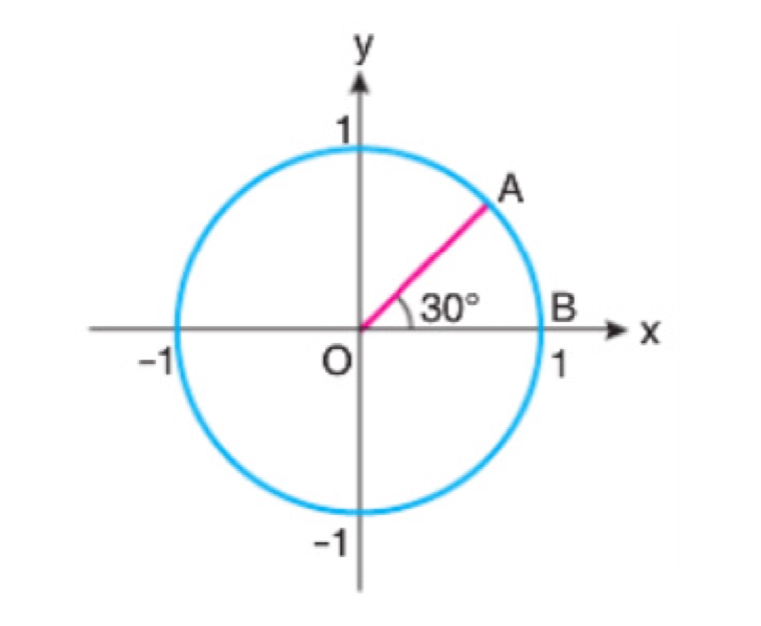
Şekildeki birim çemberde m(AOB) = 30° olduğuna göre, A noktasının koordinatlarını bulunuz.

Şekildeki birim çemberde m(AOB) = 30° olduğuna göre, A noktasının koordinatlarını bulunuz.
Çözüm: A noktasının koordinatları \( A(x,y) = A(Cos30, Sin30) = A(\frac{\sqrt{3}}{2},\frac{1}{2}) \)
Soru 5:
\( \frac{cosx}{tanx + secx } – \frac{cosx}{tanx – secx} \)
ifadesinin en sade halini bulunuz.
\( \frac{cosx}{tanx + secx } – \frac{cosx}{tanx – secx} \)
ifadesinin en sade halini bulunuz.
Çözüm:
\( \frac{cosx}{tanx + secx } – \frac{cosx}{tanx – secx} = \frac{cosx}{\frac{sinx}{cosx} + \frac{1}{cosx} } – \frac{cosx}{\frac{sinx}{cosx} – \frac{1}{cosx}} \)
\( \frac{cosx}{\frac{sinx + 1}{cosx} } – \frac{cosx}{\frac{sinx-1}{cosx}} = \frac{cosx.cosx}{sinx + 1} – \frac{cosx.cosx}{sinx-1} \)
paydaları eşitleyelim:
\( \frac{cos^2x(sinx-1)}{(sinx + 1)(sinx-1)} – \frac{cos^2x(sinx+1)}{(sinx + 1)(sinx-1)} \)
\( =\frac{cos^2x(sinx-1)}{(sin^2x – 1)} – \frac{cos^2x(sinx+1)}{(sin^2x – 1)} \)
\( =\frac{cos^2x(sinx-1)}{-cos^2x} – \frac{cos^2x(sinx+1)}{-cos^2x} \)
\( =\frac{(sinx-1)}{-1} – \frac{(sinx+1)}{-1} \)
\( =-sinx+1 + sinx+1 = 2 \)
\( \frac{cosx}{tanx + secx } – \frac{cosx}{tanx – secx} = \frac{cosx}{\frac{sinx}{cosx} + \frac{1}{cosx} } – \frac{cosx}{\frac{sinx}{cosx} – \frac{1}{cosx}} \)
\( \frac{cosx}{\frac{sinx + 1}{cosx} } – \frac{cosx}{\frac{sinx-1}{cosx}} = \frac{cosx.cosx}{sinx + 1} – \frac{cosx.cosx}{sinx-1} \)
paydaları eşitleyelim:
\( \frac{cos^2x(sinx-1)}{(sinx + 1)(sinx-1)} – \frac{cos^2x(sinx+1)}{(sinx + 1)(sinx-1)} \)
\( =\frac{cos^2x(sinx-1)}{(sin^2x – 1)} – \frac{cos^2x(sinx+1)}{(sin^2x – 1)} \)
\( =\frac{cos^2x(sinx-1)}{-cos^2x} – \frac{cos^2x(sinx+1)}{-cos^2x} \)
\( =\frac{(sinx-1)}{-1} – \frac{(sinx+1)}{-1} \)
\( =-sinx+1 + sinx+1 = 2 \)
Soru 6:
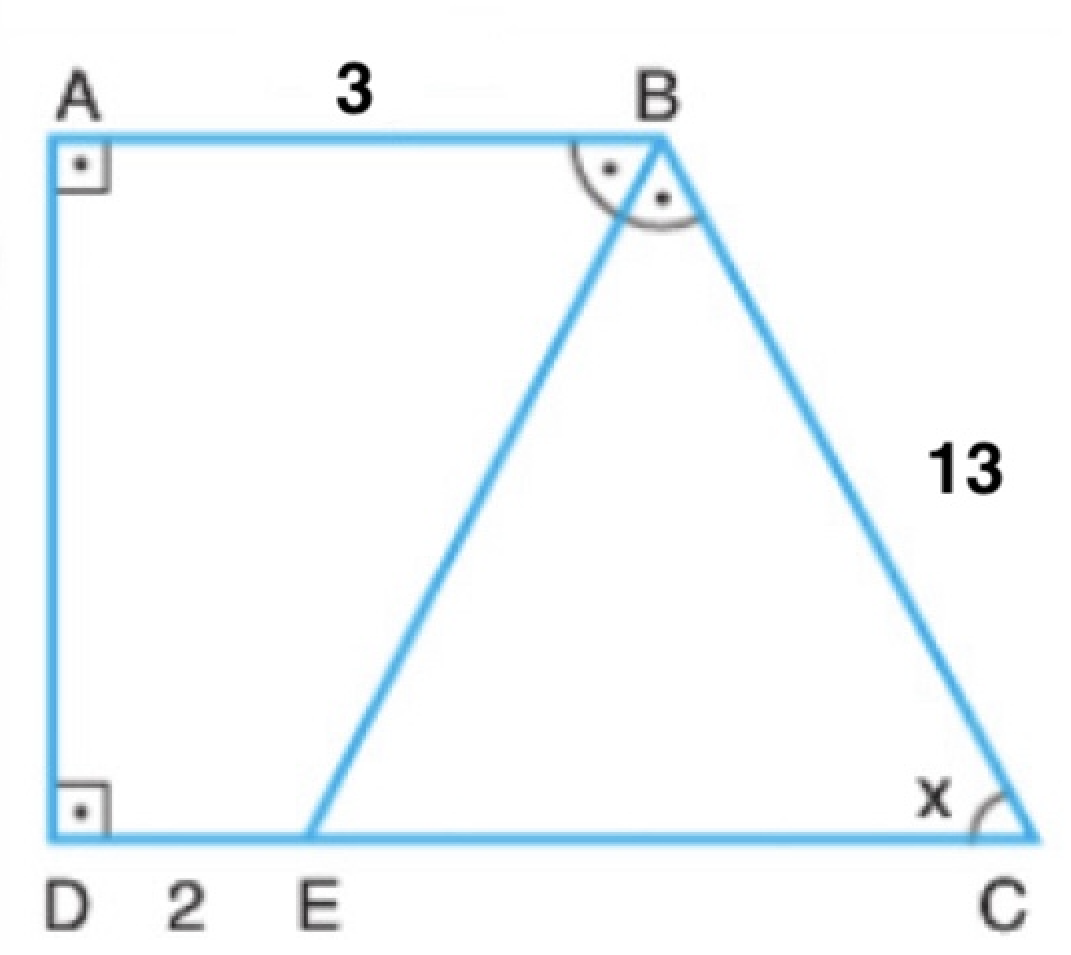
ABCD dik yamuk
|DE| = 2 br
|AB| = 3 br
|BC| = 13 br
m(ABE) = m(EBC)
m(BCE) = x
Yukarıda verilenlere göre, sin(x) değeri kaçtır?

ABCD dik yamuk
|DE| = 2 br
|AB| = 3 br
|BC| = 13 br
m(ABE) = m(EBC)
m(BCE) = x
Yukarıda verilenlere göre, sin(x) değeri kaçtır?
Çözüm:
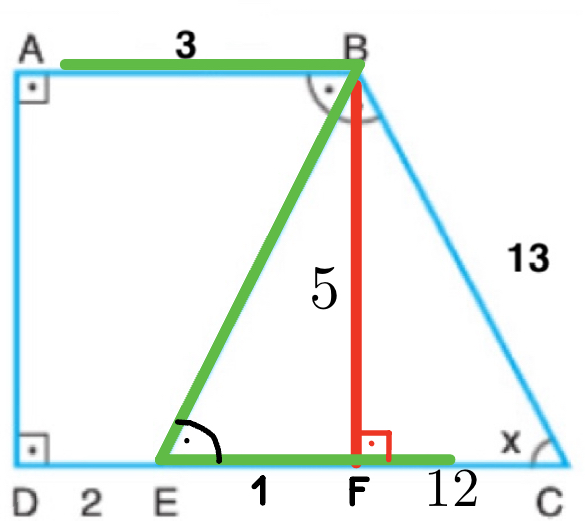
ABCD dörtgeni Dik Yamuk olduğundan; |AB| ve |DC| paraleldir. Dolayısıyla m(ABE) = m(BEC) olur. Bu durumda BEC üçgeni ikizkenar üçgen olur ve |BC| = |CE| = 13 br eşitliği bulunur. B noktasından |DC| ye dik çizelim ve bu kesim noktasına F noktası diyelim. Bu durumda ABFD dikdörtgen olur ve |AB| = |FD| = 3 br bulunur. |FD| = 3 br ise |EF| = 1 br’dir. |CE| = 13 br olduğunu daha evvel söylemiştir. Bu durumda |FC| = 12 olur ve 5-12-13 özel üçgeninden |BF| = 5 br olur. Son olarak Sinx değerini bulalım.
\( sinx = \frac{5}{13} \)

ABCD dörtgeni Dik Yamuk olduğundan; |AB| ve |DC| paraleldir. Dolayısıyla m(ABE) = m(BEC) olur. Bu durumda BEC üçgeni ikizkenar üçgen olur ve |BC| = |CE| = 13 br eşitliği bulunur. B noktasından |DC| ye dik çizelim ve bu kesim noktasına F noktası diyelim. Bu durumda ABFD dikdörtgen olur ve |AB| = |FD| = 3 br bulunur. |FD| = 3 br ise |EF| = 1 br’dir. |CE| = 13 br olduğunu daha evvel söylemiştir. Bu durumda |FC| = 12 olur ve 5-12-13 özel üçgeninden |BF| = 5 br olur. Son olarak Sinx değerini bulalım.
\( sinx = \frac{5}{13} \)
Soru 7:
\( \frac{sin(55\pi + x) + cos(80\pi – x}{cos(\frac{35\pi}{2}-x)+sin(\frac{25\pi}{2}+x)} \)
ifadesinin en sade halini bulunuz.
\( \frac{sin(55\pi + x) + cos(80\pi – x}{cos(\frac{35\pi}{2}-x)+sin(\frac{25\pi}{2}+x)} \)
ifadesinin en sade halini bulunuz.
Çözüm: Önce radyan türünden verilen açıların esas ölçülerini bulalım.
\( 55\pi = 27.2\pi + \pi\) esas ölçüsü:\(\pi\)
\(80\pi = 40.2\pi\) esas ölçücü: \( 0 \)
\( \frac{35\pi}{2} = 8.2\pi + \frac{3\pi}{2} \) esas ölçüsü: \( \frac{3\pi}{2} \)
\( \frac{25\pi}{2} = 6.2\pi + \frac{\pi}{2} \) esas ölçüsü: \( \frac{\pi}{2} \)
\( \frac{sin(\pi + x) + cos(-x)}{cos(\frac{3\pi}{2}-x)+sin(\frac{\pi}{2}+x)} \)
\( \frac{-sin(x) + cos(x)}{-sin(x)+cos(x)} = 1 \)
\( 55\pi = 27.2\pi + \pi\) esas ölçüsü:\(\pi\)
\(80\pi = 40.2\pi\) esas ölçücü: \( 0 \)
\( \frac{35\pi}{2} = 8.2\pi + \frac{3\pi}{2} \) esas ölçüsü: \( \frac{3\pi}{2} \)
\( \frac{25\pi}{2} = 6.2\pi + \frac{\pi}{2} \) esas ölçüsü: \( \frac{\pi}{2} \)
\( \frac{sin(\pi + x) + cos(-x)}{cos(\frac{3\pi}{2}-x)+sin(\frac{\pi}{2}+x)} \)
\( \frac{-sin(x) + cos(x)}{-sin(x)+cos(x)} = 1 \)
Soru 8:
\(\frac{\pi}{2} < x < \pi \) olmak üzere,
\( tanx – \frac{4 + sinx}{cosx} = 5 \)
olduğuna göre, \(cotx\) değeri kaçtır?
\(\frac{\pi}{2} < x < \pi \) olmak üzere,
\( tanx – \frac{4 + sinx}{cosx} = 5 \)
olduğuna göre, \(cotx\) değeri kaçtır?
Çözüm:
\( \frac{sinx}{cosx} – \frac{4 + sinx}{cosx} = 5 \)
\( \frac{sinx-4-sinx}{cosx} = 5 \)
\( \frac{-4}{cosx} = 5 \)
\( -4 = 5.cosx \)
\( cosx = \frac{-4}{5} \)
dar açılarından biri \(x\) olan dik üçgen çizersek 3-4-5 üçgeni olduğunu göreceğiz.
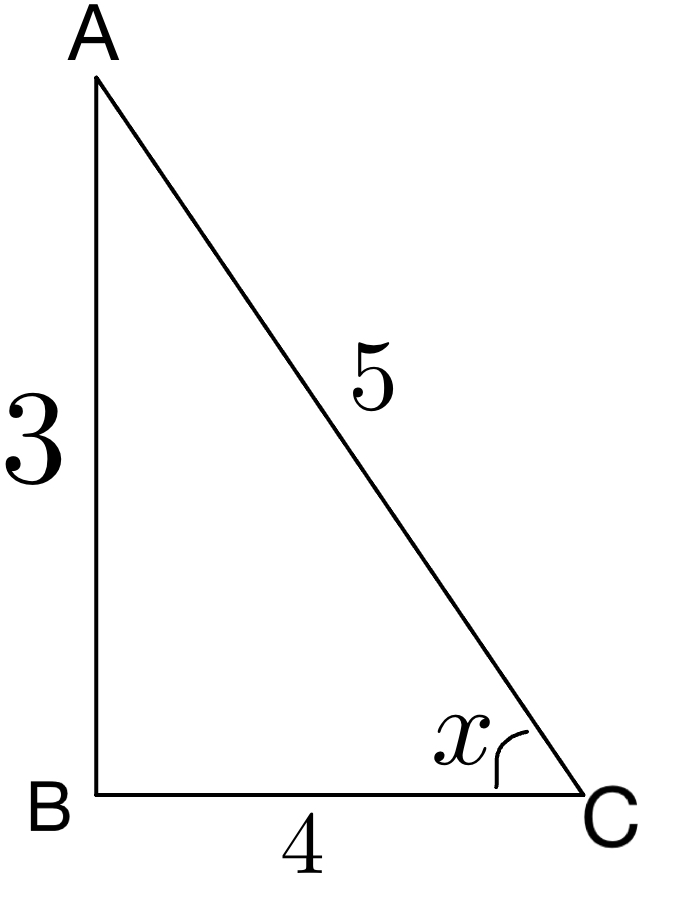
\(x\) açısı 2. bölgede olduğundan \(cotx\) değeri negatif olur.
\( cotx = -\frac{4}{3} \)
\( \frac{sinx}{cosx} – \frac{4 + sinx}{cosx} = 5 \)
\( \frac{sinx-4-sinx}{cosx} = 5 \)
\( \frac{-4}{cosx} = 5 \)
\( -4 = 5.cosx \)
\( cosx = \frac{-4}{5} \)
dar açılarından biri \(x\) olan dik üçgen çizersek 3-4-5 üçgeni olduğunu göreceğiz.

\(x\) açısı 2. bölgede olduğundan \(cotx\) değeri negatif olur.
\( cotx = -\frac{4}{3} \)
Soru 9:
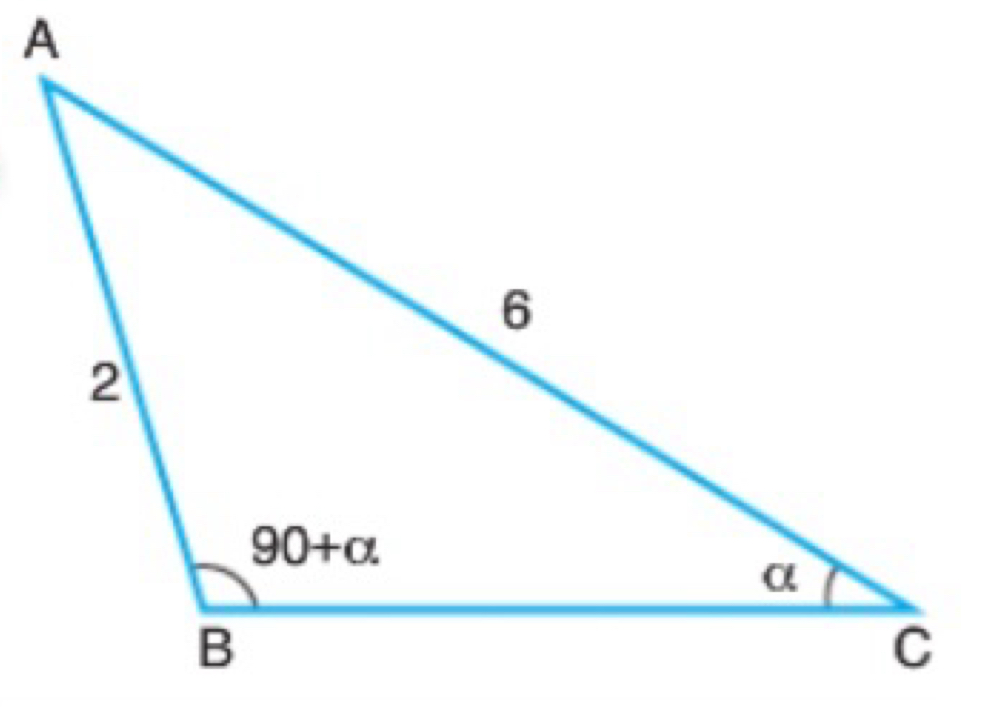
ABC üçgeninde
|AC| = 3|AB| = 6 br
m(ACB) = α
m(ABC) = 90° + α
Yukarıda verilenlere göre, cot(α) değeri kaçtır?

ABC üçgeninde
|AC| = 3|AB| = 6 br
m(ACB) = α
m(ABC) = 90° + α
Yukarıda verilenlere göre, cot(α) değeri kaçtır?
Çözüm:
\( \frac{sinα}{2} = \frac{sin(90+α)}{6} \)
\( \frac{sinα}{2} = \frac{cosα}{6} \)
\( 6.sinα = 2.cosα \)
\( \frac{6}{2} = \frac{cosα}{sinα} \)
\( cotα = 3 \)
\( \frac{sinα}{2} = \frac{sin(90+α)}{6} \)
\( \frac{sinα}{2} = \frac{cosα}{6} \)
\( 6.sinα = 2.cosα \)
\( \frac{6}{2} = \frac{cosα}{sinα} \)
\( cotα = 3 \)
Soru 10:
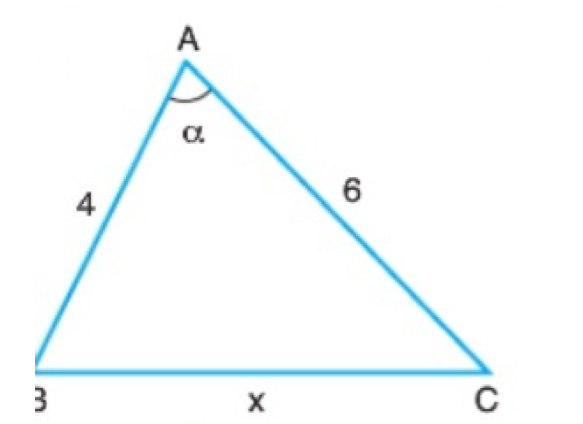
ABC üçgeninde
|AB| = 4 br
|AC| = 6 br
m(BAC) = α
\(cos(α) = \frac{1}{12}\)
olduğuna göre, |BC| = x kaç birimdir?

ABC üçgeninde
|AB| = 4 br
|AC| = 6 br
m(BAC) = α
\(cos(α) = \frac{1}{12}\)
olduğuna göre, |BC| = x kaç birimdir?
Çözüm:
\(x^2 = 4^2 + 6^2 – 2.4.6.cosα \)
\(x^2 = 16 + 36 – 48.\frac{1}{12} \)
\(x^2 = 52 – 4 \)
\(x^2 = 48 \)
\(x = \sqrt{48} \)
\(x = 4\sqrt{3} br\)
\(x^2 = 4^2 + 6^2 – 2.4.6.cosα \)
\(x^2 = 16 + 36 – 48.\frac{1}{12} \)
\(x^2 = 52 – 4 \)
\(x^2 = 48 \)
\(x = \sqrt{48} \)
\(x = 4\sqrt{3} br\)