Matematik Yazılı Örneği
10. Sınıf Matematik 1.Dönem 1. Yazılı Soruları Örneği
Soru 1:
A şehrinden B şehrine 3 farklı havayolu firması, 3 farklı otobüs firması ile yolculuk yapılabilmektedir. A şehrinden B şehrine gidip geri dönecek olan bir kişi giderken kullandığı firmayı dönüşte kullanmamak şartıyla A’dan B’ye kaç farklı şekilde gidip gelebilir?
Çözüm:
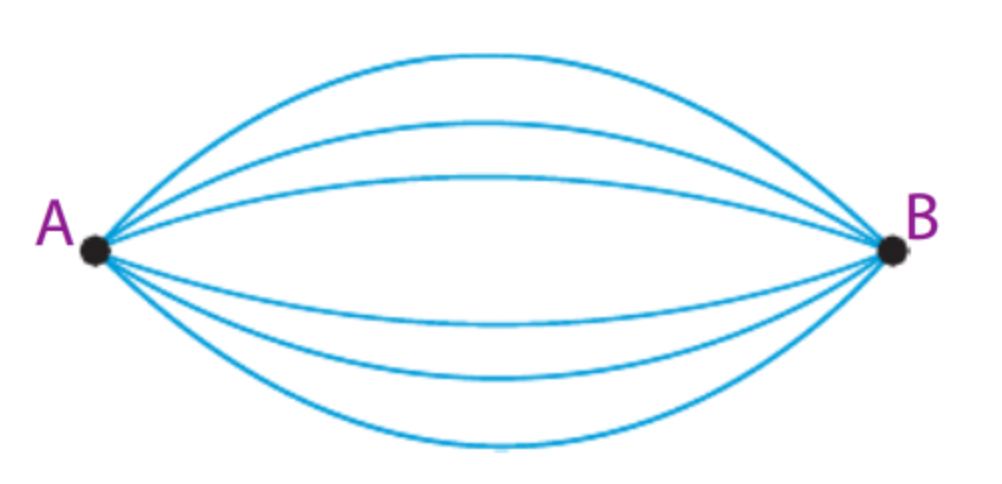
A şehrinden B şehrine toplamda 6 farklı yol var. Giderken bu 6 yoldan biri seçilecek dönüş yolunda geriye kalan 5 yoldan biri seçilecek. Bu durumda 6.5 = 30 farklı şekilde gidiş dönüş yapılabilir.

A şehrinden B şehrine toplamda 6 farklı yol var. Giderken bu 6 yoldan biri seçilecek dönüş yolunda geriye kalan 5 yoldan biri seçilecek. Bu durumda 6.5 = 30 farklı şekilde gidiş dönüş yapılabilir.
Soru 2:
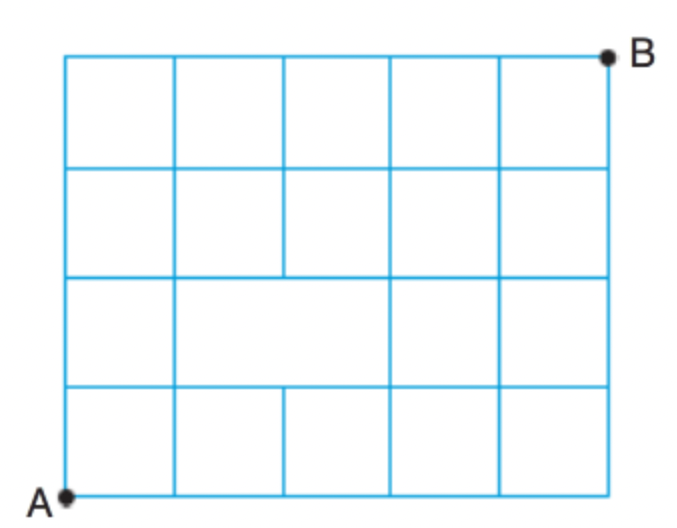
Yukarıda verilen şekilde A noktasından B noktasına çizgileri takip ederek en kısa yoldan kaç farklı şekilde gidilebilir?

Yukarıda verilen şekilde A noktasından B noktasına çizgileri takip ederek en kısa yoldan kaç farklı şekilde gidilebilir?
Çözüm:
Şekilde boşluk yokmuş gibi hesap yaparak başlayacağız ve boşluğun olduğu bölümden geçerek B noktasına kaç farklı şekilde ulaşılır bunu tüm durumlardan çıkaracağız.
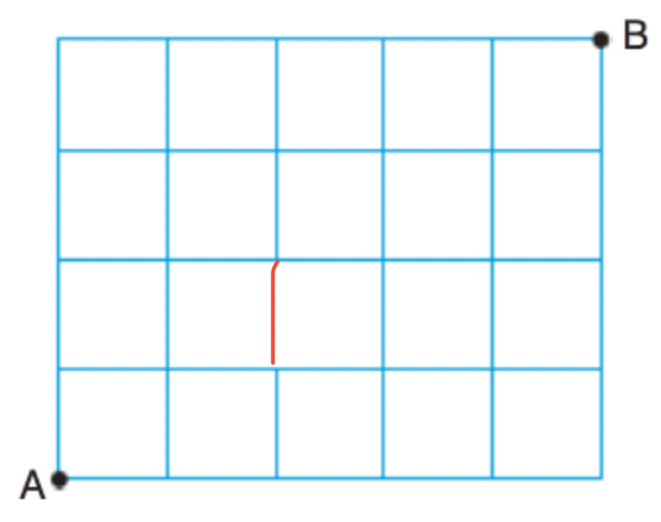
Öncelikle tüm durumları bulalım: 5 defa sağa 4 defa yukarı hareket ederek B noktasına ulaşılabilir. Soru ‘SSSSSYYYY kelimesinin harfleriyle anlamlı veya anlamsız 9 harfli kaç kelime yazılabilir?’ sorusuna dönüştü. Bu durumda:
\( \frac{9!}{5!.4!} = 126 \) A dan B ye 126 farklı şekilde gidilebilir. Yukarıdaki şekilde kırmızı ile çizdiğimiz yol aslında yok burda yapmamız gereken o yolun kullanıldığı durumları 126 dan çıkarmak. Şekli iki parçaya ayırarak hesaplayacağız.

2 defa sağa 1 defa yukarı gidersek kırmızı yolun başladığı noktaya ulaşırız. Daha sonra kırmızı yolu kullandıktan sonra:

3 defa sağa 2 defa yukarı giderek B noktasına ulaşırız.
SSY ve SSSYY harflerinin sıralanma sayısını hesaplayalım.
\(\frac{3!}{2!}.\frac{5!}{3!.2!} = 3.10 = 30 \)
kırmızı yolu kullanmak şartıyla A dan B ye 30 farklı şekilde gidilebilir.
Kırmızı yol olmadığına göre bunu tüm durumdan çıkarırsak:
\(126 – 30 = 96 \)
Şekilde boşluk yokmuş gibi hesap yaparak başlayacağız ve boşluğun olduğu bölümden geçerek B noktasına kaç farklı şekilde ulaşılır bunu tüm durumlardan çıkaracağız.

Öncelikle tüm durumları bulalım: 5 defa sağa 4 defa yukarı hareket ederek B noktasına ulaşılabilir. Soru ‘SSSSSYYYY kelimesinin harfleriyle anlamlı veya anlamsız 9 harfli kaç kelime yazılabilir?’ sorusuna dönüştü. Bu durumda:
\( \frac{9!}{5!.4!} = 126 \) A dan B ye 126 farklı şekilde gidilebilir. Yukarıdaki şekilde kırmızı ile çizdiğimiz yol aslında yok burda yapmamız gereken o yolun kullanıldığı durumları 126 dan çıkarmak. Şekli iki parçaya ayırarak hesaplayacağız.

2 defa sağa 1 defa yukarı gidersek kırmızı yolun başladığı noktaya ulaşırız. Daha sonra kırmızı yolu kullandıktan sonra:

3 defa sağa 2 defa yukarı giderek B noktasına ulaşırız.
SSY ve SSSYY harflerinin sıralanma sayısını hesaplayalım.
\(\frac{3!}{2!}.\frac{5!}{3!.2!} = 3.10 = 30 \)
kırmızı yolu kullanmak şartıyla A dan B ye 30 farklı şekilde gidilebilir.
Kırmızı yol olmadığına göre bunu tüm durumdan çıkarırsak:
\(126 – 30 = 96 \)
Soru 3:
4 farklı matematik, 3 farklı kimya ve 3 farklı fizik kitabı düz bir rafa sıralanacaktır. Aynı dersin kitapları yan yana ve matematik kitapları ortada olmak şartıyla kaç farklı şekilde sıralanabilir?
Çözüm:
Aynı tür kitapları bir paket halinde düşünmeliyiz. 3 farklı tür kitabımız var. Bu 3 paketin kendi arasında sıralamasını yaparken matematik kitapları ortada olacağı için sadece fizik ve kimya kitaplarının kendi arasındaki sıralaması önemli olacak. Aynı tür kitapların kendi içlerindeki sıralamasını da dikkate almalıyız.
Matematik kitapları kendi içinde: \(4!\)
Fizik kitapları kendi içinde: \(3!\)
Kimya kitapları kendi içinde: \(3!\)
Fizik ve Kimya kitaplarının kendi aralarındaki yer değiştirmesi: \(2\)
Sonuç: \( 4!.3!.3!.2 \)
Matematik kitapları kendi içinde: \(4!\)
Fizik kitapları kendi içinde: \(3!\)
Kimya kitapları kendi içinde: \(3!\)
Fizik ve Kimya kitaplarının kendi aralarındaki yer değiştirmesi: \(2\)
Sonuç: \( 4!.3!.3!.2 \)
Soru 4:
9 kişinin katıldığı bir yarışmada her tur 2 kişi elenecektir. 4 Turun sonunda yarışmayı kazanan kişi kaç farklı şekilde belirlenir?
Çözüm:
Her tur 2 kişi elendiğine göre ilk turda elenecek kişileri seçelim: \(C(9,2) = \frac{9.8}{2} = 36 \)
Kalan 7 kişi arasından 2. turda elenecek kişileri seçelim: \( C(7,2) = \frac{7.6}{2} = 21 \)
Kalan 5 kişi arasından 3. turda elenecek kişileri seçelim: \( C(5,2) = \frac{5.4}{2} = 10 \)
Kalan 3 kişi arasından 4. turda elenecek 2 kişiyi seçelim aynı zamanda yarışmayı kazanan kişiyi de belirlemiş olacağız:
\( C(3,2) = \frac{3.2}{2} = 3 \)
Her tur için yapılan seçimler birbirine bağlı olaylar olduğu için bulduğumuz sonuçları çarpmalıyız.
\( 36.21.10.3 \) farklı şekilde kazanan belirlenir.
Her tur 2 kişi elendiğine göre ilk turda elenecek kişileri seçelim: \(C(9,2) = \frac{9.8}{2} = 36 \)
Kalan 7 kişi arasından 2. turda elenecek kişileri seçelim: \( C(7,2) = \frac{7.6}{2} = 21 \)
Kalan 5 kişi arasından 3. turda elenecek kişileri seçelim: \( C(5,2) = \frac{5.4}{2} = 10 \)
Kalan 3 kişi arasından 4. turda elenecek 2 kişiyi seçelim aynı zamanda yarışmayı kazanan kişiyi de belirlemiş olacağız:
\( C(3,2) = \frac{3.2}{2} = 3 \)
Her tur için yapılan seçimler birbirine bağlı olaylar olduğu için bulduğumuz sonuçları çarpmalıyız.
\( 36.21.10.3 \) farklı şekilde kazanan belirlenir.
Soru 5: Aşağıda Pascal üçgeninin ilk 5 satırı verilmiştir.
Buna göre Pascal üçgeninin 8. satırının ilk üç teriminin toplamı kaçtır?
1
1
1
1
2
1
1
3
3
1
1
4
6
4
1
Buna göre Pascal üçgeninin 8. satırının ilk üç teriminin toplamı kaçtır?
Çözüm:
Pascal üçgeninde \(n.\) satır:
\( C(n-1,0) , C(n-1,1) , C(n-1,2) , … , C(n-1,n-1) \)
şeklinde hesaplanır.
8. Satırın ilk 3 terimi: \( C(7,0) , C(7,1) , C(7,2) \)
\( C(7,0) = 1 \)
\( C(7,1) = 7 \)
\( C(7,2) = \frac{7.6}{2} = 21 \)
\( 1 + 7 + 21 = 29 \)
Pascal üçgeninde \(n.\) satır:
\( C(n-1,0) , C(n-1,1) , C(n-1,2) , … , C(n-1,n-1) \)
şeklinde hesaplanır.
8. Satırın ilk 3 terimi: \( C(7,0) , C(7,1) , C(7,2) \)
\( C(7,0) = 1 \)
\( C(7,1) = 7 \)
\( C(7,2) = \frac{7.6}{2} = 21 \)
\( 1 + 7 + 21 = 29 \)
Soru 6:
\( (x – 3y)^7 \) ifadesinin \(x\) azalan kuvvetlerine göre açılımında baştan 5. terimin kat sayısı kaçtır?
\( (x – 3y)^7 \) ifadesinin \(x\) azalan kuvvetlerine göre açılımında baştan 5. terimin kat sayısı kaçtır?
Çözüm:
\( (x+y)^n\) ifadesinin \(x\) in azalan kuvvetlerine göre açılımı yapıldığında (r+1). terim:
\(C(n,r).(x)^{n-r}.y^r\) ile hesaplanır.
\(r+1 = 5\) ise \(r = 4\) ve \(n = 7\) için hesaplayalım.
(C(7,4).(x)^{3}.(-3y)^4 = \frac{7.6.5.4}{4.3.2}.x^3.(-3)^4.y^4 \)
\(35.x^3.81.y^4 \)
5. terimin katsayısı: \( 35.81 = 2835\)
\( (x+y)^n\) ifadesinin \(x\) in azalan kuvvetlerine göre açılımı yapıldığında (r+1). terim:
\(C(n,r).(x)^{n-r}.y^r\) ile hesaplanır.
\(r+1 = 5\) ise \(r = 4\) ve \(n = 7\) için hesaplayalım.
(C(7,4).(x)^{3}.(-3y)^4 = \frac{7.6.5.4}{4.3.2}.x^3.(-3)^4.y^4 \)
\(35.x^3.81.y^4 \)
5. terimin katsayısı: \( 35.81 = 2835\)
Soru 7:
A, B ve C bir deneye ait E örnek uzayının ayrık olaylarıdır.
\(P(A)·P(C’) = \frac{1}{21}, P(C) + P(B) = \frac{6}{7}\)
olduğuna göre, P(B) kaçtır?
A, B ve C bir deneye ait E örnek uzayının ayrık olaylarıdır.
\(P(A)·P(C’) = \frac{1}{21}, P(C) + P(B) = \frac{6}{7}\)
olduğuna göre, P(B) kaçtır?
Çözüm:
\(P(A) + P(B) + P(C) = P(E) \)
\(P(A) + P(B) + P(C) = 1 \)
\( P(A) + \frac{6}{7} = 1 \)
\( P(A) = \frac{1}{7} \)
\(P(A)·P(C’) = \frac{1}{21}\)
\(\frac{1}{7}·P(C’) = \frac{1}{21} \)
\(P(C’) = \frac{1}{3} \)
\(P(C) = \frac{2}{3} \)
\(P(C) + P(B) = \frac{6}{7}\)
\( \frac{2}{3} + P(B) = \frac{6}{7}\)
\( P(B) = \frac{6}{7} – \frac{2}{3} \)
\( P(B) = \frac{18}{21} – \frac{14}{21} \)
\( P(B) = \frac{4}{21}\)
\(P(A) + P(B) + P(C) = P(E) \)
\(P(A) + P(B) + P(C) = 1 \)
\( P(A) + \frac{6}{7} = 1 \)
\( P(A) = \frac{1}{7} \)
\(P(A)·P(C’) = \frac{1}{21}\)
\(\frac{1}{7}·P(C’) = \frac{1}{21} \)
\(P(C’) = \frac{1}{3} \)
\(P(C) = \frac{2}{3} \)
\(P(C) + P(B) = \frac{6}{7}\)
\( \frac{2}{3} + P(B) = \frac{6}{7}\)
\( P(B) = \frac{6}{7} – \frac{2}{3} \)
\( P(B) = \frac{18}{21} – \frac{14}{21} \)
\( P(B) = \frac{4}{21}\)