Kümeler Konu Anlatımı
Küme Tanımı
Küme iyi tanımlanmış (elemanları herkes tarafından aynı şekilde anlaşılan kısaca elemanları belirli olan) birbirinden farklı nesneler topluluğudur. Kümeler, \( A, B, C, \dots \) gibi büyük harflerle, kümenin elemanları ise \( a, b, c, \dots \) gibi küçük harflerle gösterilir. Bir \( a \) elemanı \( A \) kümesine ait ise \( a \in A \), ait değil ise \( a \notin A \) şeklinde gösterilir.
\( n \) elemanlı bir \( A \) kümesinin eleman sayısı \( s(A) = n \) şeklinde gösterilir.
Aşağıdaki ifadelerden hangisi küme belirtmez?
- A) Çift rakamlar
- B) 2’den büyük iki doğal sayı.
- C) İki basamaklı çift asal sayılar.
- D) Birler basamağı sıfır olan tam sayılar.
- E) İki basamaklı negatif tam sayılar.
B’nin elemanları belli olmadığından küme değildir.
\( A = \{1, 2, \{3, 4\}, 5\} \) kümesi ile ilgili,
- I. \( 2 \in A \)
- II. \( \{3, 4\} \notin A \)
- III. \( s(A) = 4 \)
- IV. \( A = \{1, 1, 2, \{3, 4\}, 5\} \)
- V. \( A = \{5, 1, \{3, 4\}, 2\} \)
ifadelerinden kaç tanesi doğrudur?
I, III ve V öncülleri doğrudur.
Kümeler ile ilgili her ifadede elemanların iyi tanımlanmış olması gerekir. Belirsiz eleman tanımları kümeye dahil edilmez.
Kümelerin Gösterimi
Kümeyi oluşturan elemanların önlerine nokta konarak kapalı bir şekil içerisinde gösterimlerine Venn şeması denir.
Kümeyi oluşturan elemanlar “{ }” biçimindeki parantezin içerisine aralarına virgül konularak yazılmasına liste yöntemi denir.
Kümelerdeki elemanların \(\{x \mid x\)’lerin ortak özelliği\) şeklinde gösterilmesine ortak özellik yöntemi denir.
“\(\mid\)” veya “:” sembolleri “öyle ki” anlamına gelir.
\( A = \{x \mid x \text{ tek rakam}\} \) kümesinin
a) Venn şeması ile
b) Liste yöntemi ile gösterimlerini yazınız.
a) \( A \) kümesinin Venn şeması:
1 • 3 • 5 • 7 • 9
b) Liste yöntemi: \( A = \{1, 3, 5, 7, 9\} \)
10220134 sayısındaki rakamların oluşturduğu kümenin ortak eleman özelliği ile gösterimini yazınız.
\( A = \{x \mid 0 \leq x \leq 4, x \in \mathbb{N}\} \)
\( A = \{x \mid 4 \leq x < 10, x = 2n, n \in \mathbb{Z}\} \) olduğuna göre, \( s(A) \) kaçtır?
\( A = \{4, 6, 8\} \implies s(A) = 3 \)
Sonlu ve Sonsuz Küme
Eleman sayısı doğal sayı ile ifade edilen kümeye sonlu küme denir.
Eleman sayısı doğal sayı ile ifade edilemeyen kümeye sonsuz küme denir.
Aşağıdaki kümelerin sonlu ya da sonsuz küme olup olmadıklarını bulunuz.
\( A = \{x \mid x < 6, x \in \mathbb{N}\} \)
\( B = \{x \mid x > -2, x \in \mathbb{Z}\} \)
\( C = \{x \mid 1 < x < 2, x \in \mathbb{Q}\} \)
A sonlu küme, B ve C sonsuz küme.
Boş ve Evrensel Küme
Elemanı olmayan kümeye boş küme denir ve \(\{ \}\) ya da \(\varnothing\) sembolleri ile gösterilir.
Üzerinde işlem yapılan tüm kümeleri kapsayan kümeye, o kümelerin evrensel kümesi denir ve \( E \) sembolüyle gösterilir.
Aşağıdaki kümelerden hangileri boş kümedir?
\( A = \text{Boş küme} \)
\( B = \{x \mid x < 1 \text{ ve } x \in \mathbb{R}^{+}\} \)
\( C = \{x \mid 2x + 1 = 0, x \in \mathbb{Z}\} \)
Sadece C kümesi boş kümedir.
\( A = \{2, 3, 5\} \) kümesi için aşağıdaki kümelerden hangisi evrensel küme olabilir?
a) Rakamların kümesi
b) Asal sayıların kümesi
c) Rasyonel sayıların kümesi
a, b ve c’nin hepsi olabilir.
Alt Küme
A ve B herhangi iki küme olmak üzere, A kümesinin her elemanı B kümesinin de elemanı ise A kümesine B kümesinin alt kümesi denir ve \( A \subseteq B \) ile gösterilir.
- Her küme kendisinin alt kümesidir. (\( A \subseteq A \))
- Boş küme her kümenin alt kümesidir. (\( \varnothing \subseteq A \))
- Bir kümenin kendisinden farklı tüm alt kümelerine o kümenin öz alt kümesi denir.
- A kümesi B kümesinin öz alt kümesi ise \( A \subset B \) ile gösterilir.
\( A = \{a, b, \{a\}, \{a, c\}\} \) kümesi için aşağıdakilerin doğru olup olmadığını bulunuz:
a) \( \{a\} \subset A \)
b) \( \{a, c\} \subset A \)
c) \( \{a, b\} \subset A \)
d) \( \{a, b, c\} \subset A \)
\( \{a\} \subset A \), \( \{a, b\} \subset A \), \( \{a, c\} \not\subset A \) ve \( \{a, b, c\} \not\subset A \).
\( A = \{x \mid x \leq |2|, x \in \mathbb{Z}\} \)
\( B = \{-2, 0, a, b\} \)
Kümeleri için \( B \subseteq A \) olduğuna göre, \( a + b \) toplamı kaç farklı değer alır?
\( B = \{-2, 0, a, b\} \subseteq \{-2, -1, 0, 1, 2\} \) olduğundan \( a + b = 0, 1 \text{ ve } 3 \) olabilir.
- Bir A kümesinin eleman sayısı \( n \) olmak üzere, A kümesinin alt küme sayısı: \( 2^n \).
- A kümesinin öz alt küme sayısı: \( 2^n – 1 \).
Kümelerde Kesim İşlemi
A ve B kümelerinden her ikisine de ait olan elemanların oluşturduğu kümeye A ve B kümelerinin kesim kümesi denir. Bu küme \( A \cap B \) biçiminde gösterilir:
\( A \cap B = \{ x \mid x \in A \text{ ve } x \in B \} \)
Ayrık Kümeler
A ve B kümeleri için \( A \cap B = \varnothing \) ise A ile B kümelerine ayrık kümeler denir.
- \( A \cap A = A \)
- \( A \cap (B \cap C) = (A \cap B) \cap C \)
- \( A \cap B = B \cap A \)
- \( A \cap B \subseteq A \)
- \( A \cap \varnothing = \varnothing \)
\( A = \{a, b, c, d\}, B = \{c, d, e, f\}, C = \{a, b, e, f\} \) kümeleri için aşağıdakilerden hangisi yanlıştır?
A) \( A \cap B = \{c, d\} \)
B) \( B \cap C = \{e, f\} \)
C) \( A \cap B \cap C = \varnothing \)
D) \( A \text{ ile } C \text{ ayrık.} \)
E) \( B \cap C \text{ ile } A \cap B \text{ ayrık.} \)
\( A \cap C = \{a, b\} \neq \varnothing \) olduğundan D şıkkı yanlıştır.
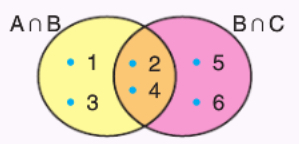
\( A \cap B \) ve \( B \cap C \) kümelerinin Venn şemasında verilen kümelere göre, B kümesinin eleman sayısı en az kaçtır?
\( 1, 2, 3, 4, 5, 6 \in B \) olduğundan B kümesinin eleman sayısı en az 6’dır.
Örnek
\( A \cap B = [-2, 5] \), \( B \cap C = [-3, 4] \) olduğuna göre, \( A \cap (C \cap B) \) kümesini bulunuz.
Çözüm
\( A \cap (C \cap B) = A \cap C \cap B = (A \cap B) \cap (B \cap C) \)
\( = [-2, 5] \cap [-3, 4] = [-2, 4] \)
Kümelerde Birleşim İşlemi
A ve B kümelerinin birleşim işlemi, bu kümelere ait tüm elemanların bir araya gelmesi ile yapılır. Matematiksel ifade olarak: \[ A \cup B = \{ x \ | \ x \in A \lor x \in B \} \]
- \( A \cup A = A \)
- \( A \cup \emptyset = A \)
- \( A \cup B = B \cup A \)
Örnek
\( A = \{ x \ | \ |x-1| \leq 1, x \in Z \} \), \( B = \{ x \ | \ -3 \leq x \leq 1, x \in Z \} \) olduğuna göre \( A \cup B \) kümesini bulunuz.
Çözüm
\( A = \{ 0, 1, 2 \}, \ B = \{ -2, -1, 0, 1 \} \)
\( A \cup B = \{ -2, -1, 0, 1, 2 \} \)
Örnek
\( A \cup B = A \) ve \( B \cap C = C \) olduğuna göre, \( A \cap B \cap C \) ve \( A \cup B \cup C \) kümelerinin eşitini bulunuz.
Çözüm
\( A \cup B = A \Rightarrow B \subseteq A \)
\( B \cap C = C \Rightarrow C \subseteq B \)
\( A \cup B \cup C = A \), \( A \cap B \cap C = C \)
Kümelerin Birleşim ve Kesişim İşlemleri
Örnek
\( A \cup B = \{ 1, 2, 3, 4, 5, 6 \} \), \( B \cup C = \{ 4, 5, 6, 7, 8 \} \) olduğuna göre, \( A \cup C \) kümesinin eleman sayısının en küçük ve en büyük değerlerini bulunuz.
Çözüm
| En Küçük | En Büyük |
|---|---|
|
\( A = \{ 1, 2, 3 \}, \ C = \{ 7, 8 \} \) \( s(A \cup C) = 5 \) |
\( A = \{ 1, 2, 3, 4, 5, 6 \}, \ C = \{ 4, 5, 6, 7, 8 \} \) \( s(A \cup C) = 8 \) |
Not
- \( A \cap (B \cup C) = (A \cap B) \cup (A \cap C) \)
- \( (B \cup C) \cap A = (B \cap A) \cup (C \cap A) \)
- \( A \cup (B \cap C) = (A \cup B) \cap (A \cup C) \)
- \( (B \cap C) \cup A = (B \cup A) \cap (C \cup A) \)
Örnek
\( A \cap B = \{ 1, 2, 3, 4, 5 \} \), \( A \cap C = \{ 2, 4, 5, 6 \} \) olduğuna göre, \( A \cap (B \cup C) \) kümesini bulunuz.
Çözüm
\( A \cap (B \cup C) = (A \cap B) \cup (A \cap C) \)
\( = \{ 1, 2, 3, 4, 5 \} \cup \{ 2, 4, 5, 6 \} \)
\( = \{ 1, 2, 3, 4, 5, 6 \} \)
Örnek
\( A \cup B = \{ a, b, c, d \} \), \( B \cup C = \{ c, d, e, f, g \} \) olduğuna göre, \( s(B \cup (A \cap C)) \) kaçtır?
Çözüm
\( B \cup (A \cap C) = (B \cup A) \cap (B \cup C) = \{ c, d \} \)
\( s(B \cup (A \cap C)) = 2 \)
Kümelerde Fark İşlemi
A ve B herhangi iki küme olmak üzere, A kümesinde bulunan fakat B kümesinde bulunmayan elemanların oluşturduğu kümeye A fark B kümesi denir.
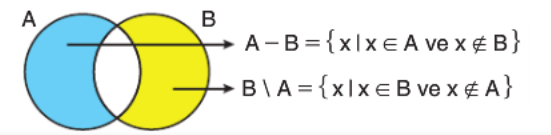
Örnek
\( A = \{ a, b, c, d, e \} \) ve \( B = \{ c, d, f, g \} \) olduğuna göre, \( A \setminus B \) ve \( B \setminus A \) kümelerini bulunuz.
Çözüm
- \( A \setminus B = \{ a, b, e \} \)
- \( B \setminus A = \{ f, g \} \)
Örnek
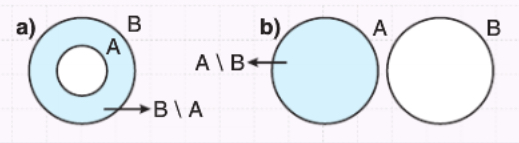
Aşağıdaki kümeleri Venn şeması ile gösteriniz.
- a) \( A \subseteq B \) için \( B \setminus A \)
- b) \( A \cap B = \emptyset \) için \( A \setminus B \)
Çözüm
Örnek
\( s(A \setminus B) = s(B \setminus A) + 8 \), \( s(A \cap B) = 8 \) ve \( s(A \cup B) = 34 \) olduğuna göre, \( s(B) \) kaçtır?
Çözüm
\( s(A \cup B) = s(A \setminus B) + s(B \setminus A) + s(A \cap B) \)
\( 34 = 8 + x + 8 + x \)
\( 34 = 16 + 2x \)
\( x = 9 \), \( s(B) = x + 8 = 17 \)
Kümelerde Tümleme İşlemi
\( E \) evrensel kümesi içinde bir \( A \) kümesi olmak üzere, \( A \) kümesinde olmayan elemanların kümesine \( A \) kümesinin tümleyeni denir ve \( A’ \) ile gösterilir.
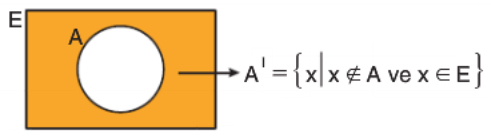
- \( A \cap A’ = \emptyset \)
- \( A \cup A’ = E \)
- \( (A’)’ = A \)
Örnek
Rakamların kümesi evrensel küme olmak üzere,
Asal sayıların kümesi \( A \),
Tek sayıların kümesi \( B \)
olduğuna göre, \( A’ \) ve \( B’ \) kümelerini bulunuz.
Çözüm
- \( A = \{ 2, 3, 5, 7 \} \Rightarrow A’ = \{ 0, 1, 4, 6, 8, 9 \} \)
- \( B = \{ 1, 3, 5, 7, 9 \} \Rightarrow B’ = \{ 0, 2, 4, 6, 8 \} \)
Örnek
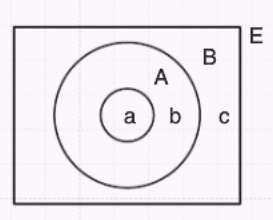
\( A \subset B \), \( s(A’) = 12 \), \( s(B \setminus A) = 4 \) olduğuna göre, \( s(B’) \) kaçtır?
Çözüm
\( b + c = 12 \)
\( b = 4 \Rightarrow c = 8 \)
\( s(B’) = c = 8 \)
Not
- \((A \cap B)’ = A’ \cup B’\) (De Morgan Kuralları)
- \((A \cup B)’ = A’ \cap B’\)
- \(A – B = A \cap B’\)
- \(B – A = B \cap A’\)
Örnek
\( (A \cup B)’ \cap B \) ve \( (A’ \cap B)’ \cup B \) kümelerinin en sade hâlini bulunuz.
Çözüm
- \((A \cup B)’ \cap B = (A’ \cap B’) \cap B = A’ \cap (B’ \cap B) = \emptyset\)
- \((A’ \cap B)’ \cup B = (A \cup B’) \cup B = A \cup (B’ \cup B) = A \cup E\)
Örnek
\( (B’ \cap A)’ \) ve \( (A \setminus B)’ \cup A \) kümelerinin eşitini bulunuz.
Çözüm
- \((B’ \cap A)’ = (B \cup A’)\)
- \((A \setminus B)’ \cup A = (A \cap B’)’ \cup A = (A’ \cup B) \cup A = A \cup B\)
Küme Problemleri
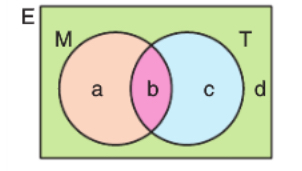
Yukarıdaki şekilde \(E\) evrensel kümesine ait \(M\) ve \(T\) alt kümeleri verilmiştir.
- \(E\): Bir sınıftaki öğrencilerin kümesi
- \(M\): Matematik dersinden geçen öğrencilerin kümesi
- \(T\): Türkçe dersinden geçen öğrencilerin kümesi
\(a\), \(b\), \(c\) ve \(d\) içinde bulunduğu kümenin eleman sayılarıdır.
- Matematik dersinden geçenlerin sayısı: \(a + b\)
- Türkçe dersinden geçenlerin sayısı: \(b + c\)
- Sadece matematik dersinden geçenlerin sayısı: \(a\)
- Sadece Türkçe dersinden geçenlerin sayısı: \(c\)
- Matematik ve Türkçe dersinden geçenlerin sayısı: \(b\)
- Matematik veya Türkçe dersinden geçenlerin sayısı: \(a + b + c\)
- Her iki dersten de kalanların sayısı: \(d\)
- En çok bir dersten geçenlerin sayısı: \(a + c + d\)
- En az bir dersten geçenlerin sayısı: \(a + b + c\)
Örnek
40 kişilik bir grupta yalnız İngilizce bilen sayısı, yalnız Japonca bilenlerin sayısının 2 katıdır. İngilizce ve Japonca bilenlerin sayısı 6, İngilizce ve Japonca bilmeyenlerin sayısı 16 olduğuna göre, İngilizce bilen kişi sayısı kaçtır?
Çözüm
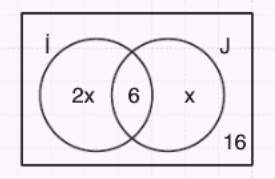
\[ 2x + 6 + x + 16 = 40 \implies x = 6 \] \[ s(i) = 18 \]
Sıralı İkili
\(a\) ve \(b\) birer reel sayı olmak üzere, \(a\) ve \(b\) ile oluşturulan \((a, b)\) ifadesine sıralı ikili denir.
- \(a \neq b \, \text{ise} \, (a, b) \neq (b, a)\)
- \((a, b) = (c, d) \, \text{ise} \, a = c \, \text{ve} \, b = d\)
Örnek
\((x – y, x) = (-2, 1)\) olduğuna göre, \(x \cdot y\) çarpımı kaçtır?
Çözüm
\(x – y = -2 \, \text{ve} \, x = 1 \implies x \cdot y = 3\)’tür.
Kartezyen Çarpımı
Birinci bileşeni \(A\) kümesinden, ikinci bileşeni \(B\) kümesinden alınarak oluşturulan tüm sıralı ikililerin kümesine \(A\) ile \(B\)’nin kartezyen çarpımı denir ve \(A \times B\) biçiminde gösterilir.
- \(A \times B = \{(a, b) \, | \, a \in A \, \text{ve} \, b \in B\}\)
- \(B \times A = \{(b, a) \, | \, b \in B \, \text{ve} \, a \in A\}\)
- \(A \neq B \, \text{için} \, A \times B \neq B \times A\)
- \(s(A \times B) = s(A) \cdot s(B) = s(B \times A)\)
Örnek
\(A \times B = \{(1, 4), (1, 3), (1, 2), (1, 1)\}\)
\(C \times A = \{(-1, 1), (0, 1)\}\)
olduğuna göre, \(B \times C\) kümesinin eleman sayısı kaçtır?
Çözüm
\(B = \{1, 2, 3, 4\}, \, C = \{-1, 0\} \, \text{olduğundan}\)
\(s(B \times C) = 4 \cdot 2 = 8\)’dir.
NOT
- \(A \times \emptyset = \emptyset \times A = \emptyset\)
- \(A \times (B \times C) = (A \times B) \times C = A \times B \times C \, \text{(Birleşme Özelliği)}\)
- \((A \times B) \cup C = (A \times C) \cup (B \times C) \, \text{(Dağılma Özelliği)}\)
- \((A \cup B) \times C = (A \times C) \cup (B \times C)\)
- \(A \times (B \cap C) = (A \times B) \cap (A \times C) \, \text{(Dağılma Özelliği)}\)
- \((A \cap B) \times C = (A \times C) \cap (B \times C)\)
Örnek
\(s(A – B) = s(A \cap B) = s(B – A) = 4\) olduğuna göre, \((A \times B) \cup (A \times A)\) kümesinin eleman sayısını bulunuz.
Çözüm
\[ (A \times B) \cup (A \times A) = A \times (B \cup A), \, s(A) = 8 \] \(s(A \cup B) = 12\) olduğundan \(s(A \times (A \cup B)) = 96\)’dır.
Kümeler Konu Anlatımı