Bölme ve Bölünebilme
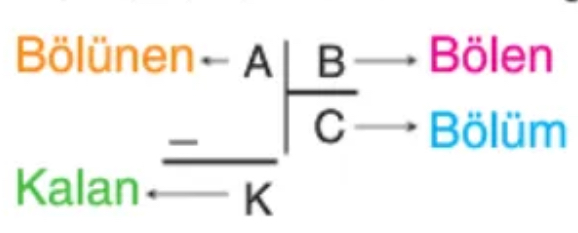
Bölme İşlemi
Bölenler Aynı İse Kalan Bulma
K, L, m, n, x, y birer pozitif tam sayı olmak üzere:
- K’nin m ile bölümünden kalan : x
- L’nin m ile bölümünden kalan : y
- K + L’nin m ile bölümünden kalan : x + y
- K − L’nin m ile bölümünden kalan : x − y
- K · L’nin m ile bölümünden kalan : x · y
- Kn‘nin m ile bölümünden kalan : xn olur.
Bölünebilme Kuralları
2 İle Bölünebilme
Birler basamağı 0, 2, 4, 6, 8 olan sayılar 2 ile tam bölünür:
- Çift sayılar 2 ile tam bölünür.
- Tek sayıların 2 ile bölümünden kalan 1’dir.
3 İle Bölünebilme
Rakamları toplamı 3 ya da 3’ün katı olan sayılar 3’e tam bölünür.
Bir sayının 3 ile bölümünden kalan, o sayının rakamları toplamının 3 ile bölümünden kalandır.
4 İle Bölünebilme
Son iki basamağı 4’ün katı ya da 00 olan sayılar 4 ile tam bölünür.
Bir sayının 4 ile bölümünden kalan, o sayının son iki basamağının 4 ile bölümünden kalandır.
5 İle Bölünebilme
Birler basamağı 0 ya da 5 olan sayılar 5 ile tam bölünür.
Bir sayının 5 ile bölümünden kalan, o sayının birler basamağının 5 ile bölümünden kalandır.
8 İle Bölünebilme
Son üç basamağı 8’in katı ya da 000 olan sayılar 8 ile tam bölünür.
Bir sayının 8 ile bölümünden kalan, o sayının son üç basamağının 8 ile bölümünden kalandır.
9 İle Bölünebilme
Rakamları toplamı 9’un katı olan sayılar 9 ile tam bölünür.
Bir sayının 9 ile bölümünden kalan, o sayının rakamları toplamının 9 ile bölümünden kalandır.
10 İle Bölünebilme
Birler basamağı 0 (sıfır) olan sayılar 10 ile tam bölünür.
Bir sayının 10 ile bölümünden kalan, o sayının birler basamağındaki rakamdır.
11 İle Bölünebilme
Bir sayının rakamları, sağdan başlayarak +, −, +, −, … şeklinde işaretlenir ve şu şekilde hesaplanır:
Sonuç 11’in katı ise sayı 11’e tam bölünür.
Aralarında Asal Sayıların Çarpımı İle Bölünebilme
Aralarında asal iki veya daha fazla sayının her birine tam bölünen sayı, bu sayıların çarpımına da tam bölünür.
Örneğin; 2 ve 3’e tam bölünen sayılar 6’ya da tam bölünür.