![Rendered by QuickLaTeX.com \subsection*{Soru 1:} \\ \\ \sqrt[4]{x - 6} + \sqrt[3]{x - 9} \\ \\ \text{İfadesi bir gerçek sayıya eşit olduğuna göre, } x \text{ aşağıdakilerden hangisine eşit olamaz?} \\ \\ \text{A) 5 \quad B) 6 \quad C) 7 \quad D) 8 \quad E) 9}](https://www.matematiknedir.com/wp-content/ql-cache/quicklatex.com-21f15b8d857a36f9e849671635d0d58c_l3.png)
Çözüm: Soruda verilen 2 köklü ifadenin de gerçek sayı olması gerekir. Kökün derecesi tek ise bu köklü ifade kökün içinde ne yazarsa yazsın bir gerçek sayıdır. Eğer kökün derecesi çift ise kökün içindeki ifadenin negatif olmaması gerekir. Bu soruda verilen ilk köklü ifadenin derecesi çift olduğu için;
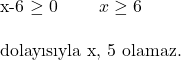
![Rendered by QuickLaTeX.com \subsection*{Soru 2:} \\ \\ \sqrt[3]{5 - x} + \sqrt[6]{x - 9} \\ \\ \text{İfadesi bir gerçek sayıya eşit olduğuna göre, } x \text{ aşağıdakilerden hangisine eşit olamaz?} \\ \\ \text{A) 12 \quad B) 11 \quad C) 8 \quad D) 10 \quad E) 9}](https://www.matematiknedir.com/wp-content/ql-cache/quicklatex.com-9ce22c0436d1f5a06a009ca89e468686_l3.png)
Çözüm: Soruda verilen 2 köklü ifadenin de gerçek sayı olması gerekir. Kökün derecesi tek ise bu köklü ifade kökün içinde ne yazarsa yazsın bir gerçek sayıdır. Eğer kökün derecesi çift ise kökün içindeki ifadenin negatif olmaması gerekir. Bu soruda verilen ikinci köklü ifadenin derecesi çift olduğu için;
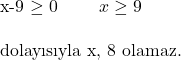
![Rendered by QuickLaTeX.com \subsection*{Soru 3:} \\ \\ \sqrt[7]{5 - x} + \sqrt{3x - 6} \\ \\ \text{İfadesi bir gerçek sayıya eşit olduğuna göre, } x \text{ aşağıdakilerden hangisine eşit olamaz?} \\ \\ \text{A) 2 \quad B) 1 \quad C) 3 \quad D) 4 \quad E) 5}](https://www.matematiknedir.com/wp-content/ql-cache/quicklatex.com-3348a0d6fd5ca283777647239444ce0e_l3.png)
Çözüm: Soruda verilen 2 köklü ifadenin de gerçek sayı olması gerekir. Kökün derecesi tek ise bu köklü ifade kökün içinde ne yazarsa yazsın bir gerçek sayıdır. Eğer kökün derecesi çift ise kökün içindeki ifadenin negatif olmaması gerekir. Bu soruda verilen ikinci köklü ifadenin derecesi çift olduğu için;
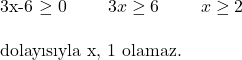
![Rendered by QuickLaTeX.com \subsection*{Soru 4:} \\ \\ \sqrt[7]{5 - x} + \sqrt{8 - 2x} \\ \\ \text{İfadesi bir gerçek sayıya eşit olduğuna göre, } x \text{ aşağıdakilerden hangisine eşit olamaz?} \\ \\ \text{A) 2 \quad B) 1 \quad C) 3 \quad D) 4 \quad E) 5}](https://www.matematiknedir.com/wp-content/ql-cache/quicklatex.com-64944fc07f1029911696e2338d81e302_l3.png)
Çözüm: Soruda verilen 2 köklü ifadenin de gerçek sayı olması gerekir. Kökün derecesi tek ise bu köklü ifade kökün içinde ne yazarsa yazsın bir gerçek sayıdır. Eğer kökün derecesi çift ise kökün içindeki ifadenin negatif olmaması gerekir. Bu soruda verilen ikinci köklü ifadenin derecesi çift olduğu için;
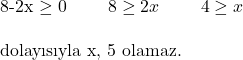
![Rendered by QuickLaTeX.com \subsection*{Soru 5:} \\ \\ \sqrt[8]{x - 1} + \sqrt{8 - 2x} \\ \\ \text{İfadesi bir gerçek sayıya eşit olduğuna göre, } x \text{ aşağıdakilerden hangisine eşit olamaz?} \\ \\ \text{A) 2 \quad B) 1 \quad C) 3 \quad D) 4 \quad E) 5}](https://www.matematiknedir.com/wp-content/ql-cache/quicklatex.com-ecd21af74f3f649187c891fcefc67596_l3.png)
Çözüm: Soruda verilen 2 köklü ifadenin de gerçek sayı olması gerekir. Kökün derecesi tek ise bu köklü ifade kökün içinde ne yazarsa yazsın bir gerçek sayıdır. Eğer kökün derecesi çift ise kökün içindeki ifadenin negatif olmaması gerekir. Bu soruda verilen iki köklü ifadenin derecesi de çift olduğu için;

![Rendered by QuickLaTeX.com \subsection*{Soru 6:} \\ \\ $x < 0 < y$ \text{ olmak üzere,} \\ \\ \sqrt[5]{x^5} - \sqrt[3]{(-y)^3} \\ \\ \text{ifadesinin eşitini bulalım:}](https://www.matematiknedir.com/wp-content/ql-cache/quicklatex.com-aaab7c70d0eec9da61ece71ade12ae82_l3.png)
Çözüm: Soruda verilen 2 köklü ifadenin de derecesi tek sayı olduğundan kök ve kuvvetleri sadeleştirirsek “x” ve “-y” ifadeleri kök dışına olduğu gibi çıkar.
![Rendered by QuickLaTeX.com x < 0 < y \\ \\ \sqrt[5]{x^5} - \sqrt[3]{(-y)^3} = x - (-y) = x + y \\ \\](https://www.matematiknedir.com/wp-content/ql-cache/quicklatex.com-c86e16eafd40e69a309e1d6ff035e3d9_l3.png)
![Rendered by QuickLaTeX.com \subsection*{Soru 7:} \\ \\ $x < 0 < y$ \text{ olmak üzere,} \\ \\ \sqrt{x^2} - \sqrt[5]{(-y)^5} \\ \\ \text{ifadesinin eşitini bulalım:}](https://www.matematiknedir.com/wp-content/ql-cache/quicklatex.com-01062adc9f71d0ca19968aaadaca1419_l3.png)
Çözüm: Soruda verilen ilk köklü ifadenin derecesi çift sayı olduğundan kök ve kuvvetleri sadeleştirirsek “x” ifadesi kök dışına mutlak değer içinde çıkar. Mutlak değerin içindeki sayı negatif ise işareti değiştirilerek yani eksi ile çarpılarak kök dışına çıkarılır.
![Rendered by QuickLaTeX.com x < 0 < y \\ \\ \sqrt{x^2} - \sqrt[5]{(-y)^5} = |x| - (-y) = -x + y \\ \\](https://www.matematiknedir.com/wp-content/ql-cache/quicklatex.com-db75b8f9d9ecc439f7697c3004e64e93_l3.png)
![Rendered by QuickLaTeX.com \subsection*{Soru 8:} \\ \\ $x < 0 < y$ \text{ olmak üzere,} \\ \\ \sqrt[4]{x^4} - \sqrt[6]{(-y)^6} \\ \\ \text{ifadesinin eşitini bulalım:}](https://www.matematiknedir.com/wp-content/ql-cache/quicklatex.com-d4fa0da06be14076afedd54f1ab18c56_l3.png)
Çözüm: Soruda verilen iki köklü ifadenin derecesi de çift sayı olduğundan kök ve kuvvetleri sadeleştirirsek “x” ve “-y” ifadeleri kök dışına mutlak değer içinde çıkar. Mutlak değerin içindeki sayı negatif ise işareti değiştirilerek yani eksi ile çarpılarak kök dışına çıkarılır.
![Rendered by QuickLaTeX.com x < 0 < y \\ \\ \sqrt[4]{x^4} - \sqrt[6]{(-y)^6} = |x| - |-y| = -x - y \\ \\](https://www.matematiknedir.com/wp-content/ql-cache/quicklatex.com-e057b23945993f1983f11de585bfe42e_l3.png)
![Rendered by QuickLaTeX.com \subsection*{Soru 9:} $x < 0 < y$ \text{ olmak üzere,} \\ \\ \sqrt{(-x)^2} - \sqrt[5]{y^5} + \sqrt{y^2 - 2xy + x^2} \\ \\ \text{ifadesinin eşitini bulalım:}](https://www.matematiknedir.com/wp-content/ql-cache/quicklatex.com-cfbdf2214484663db7d32441033d6b7c_l3.png)
Çözüm: Önceki sorulardan farklı olarak burada verilen 3. ifade 3 terimli bir ifadedir ve tam kare bir ifadedir. Tam kareye dönüştürdükten sonra aynı yöntemler soru çözülür.
![Rendered by QuickLaTeX.com x < 0 < y \\ \\ \sqrt{y^2 - 2xy + x^2} = \sqrt{(y-x)^2} \\ \\ \sqrt{(-x)^2} - \sqrt[5]{y^5} + \sqrt{(y-x)^2} = |-x| - y + |y-x| = - x - y + y - x = -2x \\ \\](https://www.matematiknedir.com/wp-content/ql-cache/quicklatex.com-6ff83b0b008fe0f4c2e6caa2948c508a_l3.png)