
Çözüm: Köklü iki sayıyı toplarken veya çıkarırken köklü sayıların dereceleri ve kökün içindeki sayıların aynı olması gerekir. Böyle bir durumda katsayılar arasında toplama veya çıkarma işlemi yapılır.
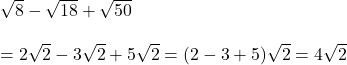
![Rendered by QuickLaTeX.com \subsection*{Soru 2:} \\ \\ \sqrt[3]{54} - \sqrt[3]{128} + \sqrt[3]{250} \\ \\ \text{işleminin sonucunu bulalım.}](https://www.matematiknedir.com/wp-content/ql-cache/quicklatex.com-0e1f4b43d28618c1d40df7d17ec39a9a_l3.png)
Çözüm: Köklü iki sayıyı toplarken veya çıkarırken köklü sayıların dereceleri ve kökün içindeki sayıların aynı olması gerekir. Böyle bir durumda katsayılar arasında toplama veya çıkarma işlemi yapılır.
![Rendered by QuickLaTeX.com \sqrt[3]{3^3 \cdot 2} - \sqrt[3]{4^3 \cdot 2} + \sqrt[3]{5^3 \cdot 2} \\ \\ = 3\sqrt[3]{2} - 4\sqrt[3]{2} + 5\sqrt[3]{2} \\ \\ = (3-4+5)\sqrt[3]{2} = 4\sqrt[3]{2}](https://www.matematiknedir.com/wp-content/ql-cache/quicklatex.com-2c046090c84871242265ab44ff6b9e65_l3.png)
![Rendered by QuickLaTeX.com \subsection*{Soru 3:} \\ \\ \sqrt{7 - \sqrt[3]{64}} - \sqrt{18 + \sqrt{81}} + \sqrt{15 - \sqrt[4]{81}} \\ \\ \text{işleminin sonucunu bulalım.}](https://www.matematiknedir.com/wp-content/ql-cache/quicklatex.com-20eb84ab2b552ca564af2d841d8a4c5b_l3.png)
Çözüm: Köklü iki sayıyı toplarken veya çıkarırken köklü sayıların dereceleri ve kökün içindeki sayıların aynı olması gerekir. Böyle bir durumda katsayılar arasında toplama veya çıkarma işlemi yapılır. Bu şekilde iç içe kökler olduğunda en içteki köklü ifadeden başlanır.
![Rendered by QuickLaTeX.com \sqrt{7 - \sqrt[3]{64}} = \sqrt{7 - \sqrt[3]{4^3}} = \sqrt{7 - 4} = \sqrt{3} \\ \\ \sqrt{18 + \sqrt{81}} = \sqrt{18 + \sqrt{9^2}} = \sqrt{18 + 9} = \sqrt{27} = \sqrt{3^2.3} = 3\sqrt{3}\\ \\ \sqrt{15 - \sqrt[4]{81}} = \sqrt{15 - \sqrt[4]{3^4}} = \sqrt{15 - 3} = \sqrt{2^2.3} = 2\sqrt{3} \\ \\ \sqrt{7 - \sqrt[3]{64}} - \sqrt{18 + \sqrt{81}} + \sqrt{15 - \sqrt[4]{81}} = ? \\ \\ \sqrt{3} - 3\sqrt{3} + 2\sqrt{3} = (1 - 3 + 2)\sqrt{3} = 0](https://www.matematiknedir.com/wp-content/ql-cache/quicklatex.com-036868e254990d52c3e218c8e140d75f_l3.png)
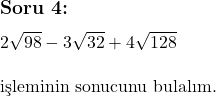
Çözüm: Köklü iki sayıyı toplarken veya çıkarırken köklü sayıların dereceleri ve kökün içindeki sayıların aynı olması gerekir. Böyle bir durumda katsayılar arasında toplama veya çıkarma işlemi yapılır.
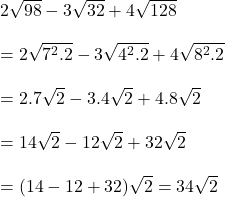
Diğer köklü sayı yazılarına buradan ulaşabilirsiniz.